この記事は素数大富豪 Advent Calendar 2022 - Adventarの17日目の記事です。
みなさんこんにちはmickeyです!
昨日の記事は、北大素数大富豪同好会さんの「北大祭に出展した話2022 」ですね。僕はまだ対面で素数大富豪をしたことがないので、次回は是非参加してみたいです*1。
さて今回は、まだまだ未開拓な合成数だしの新しい戦術を思いついたので書いてみます。
その名も、「指数表記多用型合成数」そして「平方数型合成数」です。二つとも、記憶量を節約でき、かつ出しやすい合成数です。特に、この記事では最も使用頻度が高くなると思われる7枚だし合成数を紹介します!実はブログを書くのは初めてなので、おそらく日本語がおかしいところがあると思いますが、お許しください…
ではさっそく見ていきましょう!
第一章 指数表記多用型合成数とは
まずは具体例をどうぞ
15T8769=13^4×23^2
J881376=2^5×13^5
(1188K76)
1T89567=223^3
T673289=3^6×11^4
9948825=3^4×5^2×17^3
9858192=2^4×3×59^3
9653618=2×13^6
9624416=2^5×67^3
8934121=7^4×61^2
8489664=2^6×3^3×17^3
6928416=2^5×3^9×11
6889792=2^6×7^2×13^3
6885376=2^12×41^2
6718464=2^10×3^8
6613488=2^4×3^10×7
6588344=2^3×7^7
5971968=2^13×3^6
4782969=3^14
4574296=2^3×83^3
3188646=2×3^13
2985984=2^12×3^6
1997568=2^8×3^3×17^2
1889568=2^5×3^10
1679616=2^8×3^8
1469664=2^5×3^8×7
1259712=2^6×3^9
1179648=2^17×3^2
ざっと25個*2。名前の通り、素因数分解した時に、指数表記がたくさん出てくるのが特徴です。このうちの5つでも覚えると*3、かなり役に立ちます。
さて、では何故この合成数が便利なのかというと、「出し方のパターンがたくさんある」
からなんです。例えば、
1179648=2^17×3^2=2^10×2^7×3×3=2^5×2^6×2^6×3×3=2^12×2^5×3^2
といったように、素因数部分の組み合わせの自由度がとても高いことがわかります。まだまだ未開拓分野なので、みなさんもオリジナルの形を見つけてみて下さい!
第二章 平方数型合成数とは
まずは具体例をどうぞ
96983T4=2^6×1231^2
9T68849=3^2×3181^2
38618Q9=5623^2
15T8769=13^4×23^2
J978521=3461^2
J648569=3413^2
T673289=3^6×11^4
3865T89=6217^2
8934121=7^4×61^2
8596624=2^4×733^2
7436529=3^6×101^2
7198489=2683^2
6885376=2^12×41^2
6859161=3^6×97^2
6718464=2^10×3^8
6395841=3^4×281^2
5841889=2417^2
5678289=2383^2
4946176=2^8×139^2
4897369=2213^2
4782969=3^14
4464769=2113^2
3485689=1867^2
2614689=3^2×7^4×11^2
2455489=1567^2
1776889=31^2×43^2
1679616=2^8×3^8
1347921=3^6×43^2
ざっと28個*4。名前の通り、完全平方になっている合成数です。そしてこの完全平方という形にさまざまなメリットがあるんです。
メリット1 計算力があれば素因数しか覚える必要がない
まずは、X^2を簡単に計算する方法を紹介します。先に一般形から
X^2=X^2−Y^2+Y^2=(X+Y)(X−Y)-Y^2 (X.Y∈NかつX>Y)
中学校で習う因数分解です。これをうまーく使うと計算が一瞬で終わります。
例えば、
2213^2=2213^2−13^2+13^2=(2213+13)(2213−13)+13^2=2226×2200+13^2=4897200+169=4897369
はい。簡単ですね*5*6*7*8。こうすると、素因数部分しか覚える必要がないので記憶量を節約できます。
メリット2 一つの合成数から派生可能
さて、ここからがこの合成数の真髄です。そもそも合成数を大量に覚えづらい理由として、四つ子素数のように似た形を作るのが難しいという点があります。それを破壊するのがこの平方数型合成数です。なんと、フェルマー法を用いることにより大量に派生形を作ることができます。
まず、フェルマー法とはある数がX^2−Y^2だとわかっている時、簡単に素因数分解する方法です。例えば
899=30^2−1^2=(30+1)(30−1)=31×29
このように、899が30^2−1^2だと気付くことができれば、簡単に素因数分解できます。これを用いると、平方数型合成数から平方数を引いて、簡単に派生形を量産することができます。例えば
4897368=4897369−1=2213^2−1^2=(2213+1)(2213−1)=(2214)×(2212)=(2×3^3×41)(2×2×7×79)=2^3×3^3×7×41×79
4897365=4897369−4=2213^2−2^2=(2213+2)(2213-2)=(2215)(2211)=(5×443)(3×11×67)=3×5×11×67×443
4897353=4897369−16=(2217)(2209)=3×47^2×739
4897344=4897369−25=(2218)(2208)=2^6×3×23×1109
このように、たった一つの合成数からたくさん派生系を作れました。4桁の素因数分解がすぐできる人は素因数部分を覚える必要がないので、記憶量を節約することができます*9。
フェルマー法による派生はまだまだ調べ切れていないので、是非皆さんも好きな合成数で調べてみて下さい!
さて、もうお気づきの方もいらっしゃるかもしれません。そう、指数表記多用型合成数であり平方数型合成数でもある合成数が存在します。以下がその例
15T8769=13^4×23^2
T673289=3^6×11^4
8934121=7^4×61^2
7436529=3^6×101^2
6885376=2^12×41^2
6859161=3^6×97^2
6718464=2^10×3^8
4782969=3^14
2985984=2^12×3^6
1679616=2^8×3^8
1347921=3^6×43^2
最大素因数が大きめなものは省きました。この合成数達は上記の二つの合成数の特徴を同時に備えているため非常に使いやすいです。
特に、この中でも6718464=2^10×3^8と4782969=3^14の使いやすさは群を抜いています。ということで、この二つの合成数について軽く紹介します。
4782969=3^14
素因数のみでしか3を使わないので、指数部分でかなり遊べます。フェルマー法で派生させると、
4782968=4782969−1=2^3×547×1093となり、4782969=3^4×3^10よりも多くの札を消費できます。
4782965=4782969−4=5×11×19×23×199となり、9を4枚処理できます。
4782944=4782969−25=2^5×137×1091となり、2^5の部分で若干遊べます。
4782888=4782969−81=2^3×3^4×11^2×61となり、指数表記が多めで、8を4枚処理できます。
4782869=4782969−100=7×13^3×311となり、余分なKとJを同時に処理できます
3782969=4782969−1000000=1187×3187となり、半素数なので計算しやすいです。8を3枚処理できます。
6718464=2^10×3^8
これも、素因数のみでしか2と3を使わない便利な合成数です。偶数消費量も多いため、個人的には今日紹介した合成数の中でも一番出しやすいと思います。フェルマー法派生は
6718463=6718464−1=2591×2593となり構成する札が、(112233455667899)なので手札を大量に処理したい時に重宝します。
6718448=2^4×11×59×647となり、偶数処理量が多い合成数です。
6718439=6718464−25=7^2×13×53×199となり、6718464=2^9×2×3^8で最大でも1枚しか処理できない9を3枚処理できます。
5718464=6718464−1000000=2^6×199×449となり、4を4枚、9を3枚処理出来ます。
- 第4章 実戦編
では、実戦でどのように使用するかを説明します。基本的には両プレイヤーが全出しに失敗した後(手札枚数は24〜25枚)に
という手順で手札を処理します。上記の合成数で使う札の枚数はおよそ10〜15枚なので、合成数→7枚14桁素数、で使う札の枚数は17〜22ということになります。よって残り枚数は2〜8枚です。結構組み切れそうですね*10。
---
2023.8.6追記
この組み切りで使う7枚14桁素数の素数表を投稿しました。https://mickey57.hatenablog.com/entry/2023/08/06/022239?_gl=1*sjwq21*_gcl_au*MTUwNjAzNDQ0OC4xNjkxMjM4NjA4&_ga=2.186922152.1071269765.1691238554-735783007.1689835576
こちらも併せてご覧ください。
---
最後に実戦をお見せします
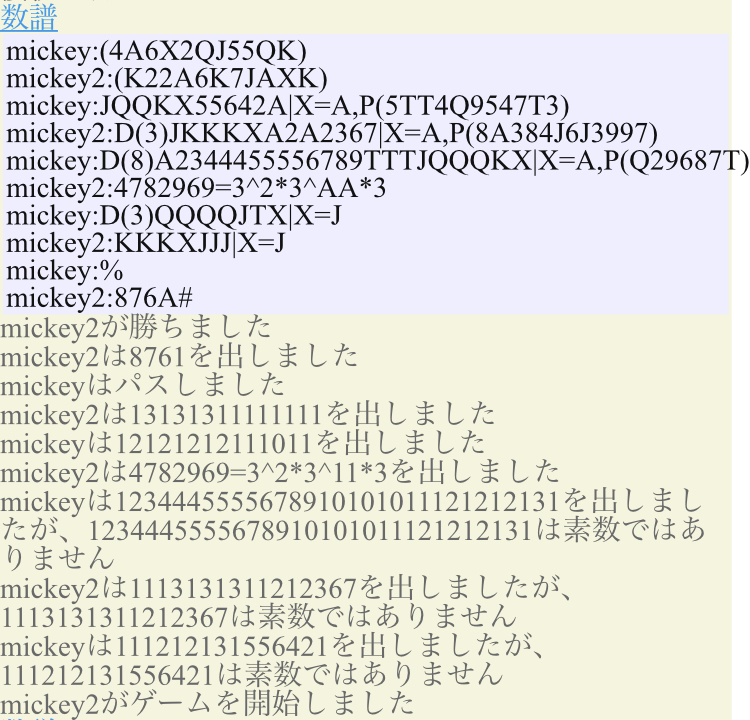
これは4782969=3^2×3^11×3→KKKJJJJ→8761の組み切りです。
このように、指数部分の組み合わせを即興で作れれば、組み切りの可能性も上がると思います。
第5章 最後に
現在の素数大富豪環境では、7枚だしラリー戦術は警戒されすぎて使いづらくなっています。なので、今後7枚だしで攻める時は基本的に合成数出しを絡めた組み切りになるのかなー、と思っています。この記事を見た人は、是非7枚だし合成数を研究してみてください。
さて、明日の記事ははちさんの「はち杯について」です。僕は第7回の合成数大富豪の大会*11に出場したのですが、ぼっこぼこにされてしまいました*12。次回までに色々対策を練って、次こそは優勝したいです。
以上で記事は終わりです。質問や指摘、訂正等ありましたら、お手数をおかけしますがmickeyのTwitter(@Factorization57)にご連絡下さると助かります。
最後までお読み下さりありがとうございました。
*1:北海道に行ったことすらないですけど…
*2:これでもかなり厳選した方です…全て4枚以上の被りがなく、偶数消費が多めのものを厳選しました
*3:最初に覚えるのは、2^x×3^yの形をオススメします
*4:この合成数も、4枚以上の被りがなく偶数消費が多いものを厳選しました
*5:いうほど簡単か?
*6:計算を楽にするコツは、10の倍数を作ることです
*7:もっと計算が楽になる例を一応載せときます。97^2=97^2−3^2+3^2=(97+3)(97-3)+3^2=100×94+9=9409
*8:2226×2200は気合いで計算します。2226×2200=2200^2+2200×26=4840000+57200=4897200と計算すればもっと楽に計算できます
*9:反素数に派生できるものなら、あまり計算力がなくても即興で派生させられると思います
*10:僕は、全出し後に勝ち確定組み切りをする際、15回に1回くらいの割合でこの合成数を使って組み切ります
*11:
*12:超楽しかったので毎月開いてほしいぐらいです(無茶)